Hukum II Termodinamika dan Aplikasinya

A. INDIKATOR

3.7.1 Mengimplementasikan hukum II termodinamika dalam kehidupan sehari-hari

3.7.2 Menemukan koherensi antara mesin pemanas carnot dengan mesin pendingin carnot

3.7.3 Menggunakan formula besaran-besaran pada mesin carnot

B TUJUAN PEMBELAJARAN

1. Melalui kegiatan diskusi siswa diharapkan dapat memahami hukum II termodinamika

2. Melalui kegiatan presentasi siswa diharapkan dapat mengaplikasikan hukum II termodinamika pada mesin carnot

3. Melalui kegiatan latihan soal siswa diharapkan dapat menentukan nilai efisiensi pada mesin carnot

C. MATERI AJAR

1) Peta Konsep

Gambar 3.1 Peta Konsep Pertemuan 3

2) Materi

a) Hukum II Termodinamika

Hukum I termodinamika menyatakan bahwa energi bersifat kekal. Energi tidak dapat diciptakan dan tidak dapat dimusnahkan melainkan hanya dapat berubah dari satu bentuk energi menjadi bentuk energi yang lainnya. Sedangkan mengenai perubahan energi mana yang bisa berlangsung merupakan batasan yang akan dibahas dalam hukum II termodinamika.

Hukum II termodinamika menyatakan bahwa, “tidak mungkin ada proses yang menyerap kalor dari reservoir pada satu temperatur kemudian mengubah seluruh kalor menjadi usaha mekanis”. Pernyataan ini berarti bahwa tidak ada satu pun mesin kalor yang benar-benar sempurna. Salah satu contohnya adalah AC. Benda yang satu ini tidak akan mungkin mengubah kalor seluruhnya menjadi kerja, pasti akan ada kalor yang dibuang oleh AC.

b) Mesin Kalor

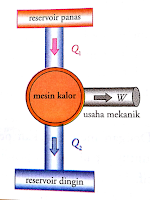
Mesin kalor adalah mesin yang mengubah sebagian panas menjadi kerja. Mesin kalor bekerja dengan dua reservoir, yaitu reservoir suhu tinggi dan rendah. Mesin kalor menyerap kalor dari reservoir suhu tinggi kemudian mengalirkan sebagian kalor tersebut ke reservoir suhu rendah dan sebagiannya lagi diubah menjadi usaha mekanik. Skema mesin kalor bisa dilihat pada gambar di bawah ini.

Gambar 3.1 Skema Mesin Kalor

Kalau ingin mengubah nilai Q1   menjadi W semua, itu tidak akan mungkin tercapai, karena pasti akan selalu ada kalor yang dibuang. Banyak sedikitnya kalor yang dibuang, tergantung efisiensi mesin kalor tersebut.

Efisiensi mesin kalor yang biasa disimbolkan dengan η didefinisikan sebagai rasio antara W yang dihasilkan dengan dengan kalor yang diberikan pada reservoir suhu tinggi Q1. Secara matematis, dapat dirumuskan dengan,

Karena nilai usaha pada mesin kalor senilai,

Sehingga, untuk menghitung nilai efisiensi mesin kalor juga bisa dengan rumusan,

Setiap mesin pun pasti mempunyai yang namanya koefisien kinerja. Mesin kalor yang baik adalah mesin yang dapat menyerap banyak kalor dalam reservoir suhu tinggi dan mengubah sebagian kalor tersebut menjadi kerja dalam jumlah yang sedikit. Dimana, semakin besar nilai koefisien kinerjanya maka akan semakin baik pula kinerja mesin tersebut. Untuk menentukan koefisien kinerja mesin kalor, menggunakan rumus berikut:

Keterangan:

Kp = koefisien kinerja

Koefisien kinerja suatu mesin kalor juga bisa dicari dengan rumus,

c) Mesin Pendingin

Mesin pendingin merupakan mesin kalor yang beroperasi secara terbalik. Jika mesin kalor mengambil kalor dari reservoir suhu tinggi dan melepaskannya ke reservoir suhu rendah, maka mesin pendingin melakukan hal yang sebaliknya, yaitu mengambil kalor dari reservoir suhu rendah (di dalam refrigerator) dan melepaskannya ke reservoir suhu tinggi (udara sekitar, di luar mesin pendingin).

Jika mesin kalor menghasilkan usaha mekanik, justru mesin pendingin memerlukan usaha dari luar untuk kelangsungan operasionalnya. Usaha luar tersebut dapat berupa energi listrik di rumah kita. Berikut skema aliran energi sebuah mesin pendingin.

Gambar 3.3 Skema mesin pendingin

Mesin pendingin yang baik adalah mesin yang dapat memindahkan kalor sebanyak mungkin dari dalam pendingin dengan usaha mekanik yang sekecil-kecilnya. Ini yang disebut dengan koefisien kinerja, yaitu rasio antara kalor yang diserap dari reservoir suhu rendah dengan besarnya usaha yang diperlukan. Secara matematis dapat dirumuskan dengan,

Keterangan:
Kd = koefisien kinerja

Koefisien kinerja suatu mesin pendingin juga bisa dicari dengan rumus,

d) Mesin Carnot

Menurut hukum II Termodinamika, tidak ada mesin kalor yang dapat memiliki efisiensi senilai 100%. Jika kita memiliki dua reservoir suhu tinggi dan reservoir suhu rendah, berapakah nilai efisiensi yang dimiliki? Pertanyaan inilah yang pertama kali dijawab oleh seorang ilmuwan asal Prancis, yaitu SADI CARNOT pada tahun 1924.

Sadi Carnot mengembangkan mesin kalor dengan efisiensi maksimum yang masih memenuhi hukum II termodinamika. Beliau memperkenalkan metode baru untuk meningkatkan efisiensi mesin. Nama mesin tersebut adalah mesin carnot. Dan nama siklusnya adalah siklus carnot.

e) Siklus Carnot

Siklus adalah serangkaian proses yang dimulai dari suatu keadaan awal dan berakhir pada keadaan yang sama dengan keadaan awalnya. Agar dapat melakukan usaha terus-menerus, suatu sistem harus bekerja dalam satu siklus. Pada siklus carnot terdiri atas dua proses isotermik dan dua proses adiabatik.Perhatikan gambar berikut.

Gambar 3.4 Siklus Carnot

Proses a-b

Gas memuai secara isotermal pada suhu Tp atau T1  (suhu tinggi) dan menyerap kalor Qp atau Q1  (kalor pada suhu tinggi). Pada proses ini gas menyerap kalor pada temperatur tinggi. Suhu sistem sama dengan suhu reservoir panas, sehingga disebut proses isotermik. Gas memuai dan melakukan usaha pada pengisap. Karena energi dalam tetap, maka usaha yang dilakukan pada sistem sama dengan kalor yang diserap.

Proses b-c

Gas memuai secara adiabatik sampai suhu gas turun ke Td atau T2  (suhu rendah). Pada proses ini beban pengisap dikurangi, sehingga gas memuai menurut proses adiabatik. Terjadi pengurangan energi dalam dan suhu sistem menurun sampai sama dengan suhu pada reservoir dingin sambil melakukan usaha.

Proses c-d

Gas termampatkan secara isotermal pada Td atau T2  dan mengeluarkan kalor |Qd| atau |Q2|  (kalor pada suhu rendah). Gas mengalami penyusutan dengan membuang kalor pada reservoir dingin sehingga usahanya bernilai negatif.

Proses d-a

Gas termampatkan secara adiabatik kembali ke keadaan awal pada suhu Tp atau T1. Beban pengisap ditambah, sehingga gas menyusut. Pada proses ini terjadi penambahan energi dalam dan suhu naik sampai dengan suhu pada reservoir panas. Energi dalam gas kembali pada keadaan awal siklus.

Karena di dalam mesin carnot adalah gas ideal, kita dapat menghitung efisiensi mesin. Karakteristik mesin carnot dinyatakan dengan efisiensi mesin yaitu perbandingan antara usaha yang dilakukan dengan kalor yang diserap. Secara matematis sudah diketahui pada pembahasan mesin kalor. Namun, khusus siklus carnot! Rasio kalor di antara dua reservoir sama dengan perbandingan suhunya. Sehingga, secara matematis dapat dituliskan,

Sehingga nilai efisiensi menjadi,

Untuk lebih jelasnya mengenai siklus carnot, silahkan tonton video di bawah ini:

f) Entropi

Penambahan panas pada suatu benda akan meningkatkan ketidakteraturan pada sistem karena akan menambah kecepatan molekul rata-rata serta keacakan gerak molekul. Contohnya adalah ekspansi pada gas. Ekspansi pada gas juga akan menimbulkan ketidakteraturan karena molekul akan mengalami keacakkan lebih besar setelah mengalami ekspansi. Contoh lain adalah kristal. Sistem zat padat yang partikel-partikelnya saling berdekatan mempunyai keteraturan yang tinggi, atau dengan kata lain entropinya rendah.

Dengan penjelasan di atas, dapat kita pahami bahwa entropi adalah suatu ukuran ketidakteraturan sistem. Semakin suatu sistem tidak teratur, maka akan semakin tinggi entropinya. Sistem pada gas yang memiliki partikel-partikel yang saling berjauhan, pasti memiliki keteraturan yang rendah, atau dengan kata lain tingkat entropinya tinggi.

Entropi termasuk fungsi keadaan, sehingga harga entropi hanya dilihar dari keadaan awal dan akhirnya saja. Tidak bergantung pada lintasan yang ditempuh. Perubahan entropi pada suatu sistem dapat dirumuskan sebagai berikut.

Jika entropi pada suatu sistem meningkat maka nilai  akan positif. Begitupun sebaliknya, jika entropi pada suatu sistem menurun, maka nilai  akan negatif.